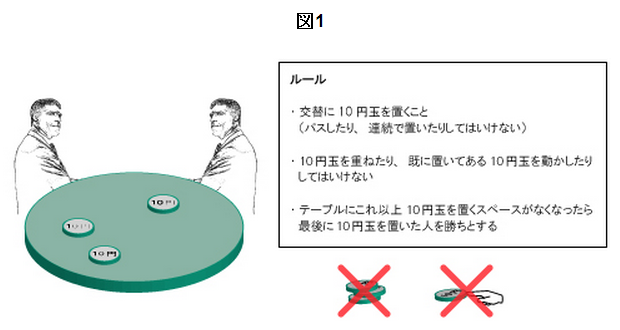
目覚めるとそこには巨大な丸いテーブル、大量に積まれた10円玉硬貨、そして不敵な笑みを浮かべる悪魔がいた。「ゲームをしよう」そう悪魔が切り出した。細長い手でテーブルを指さしながら「ルールは至って簡単だ。この上に10円玉を重ならないよう交替に置き、これ以上10円玉を置くスペースがなくなったらその人の負けとする。念のため正確なルールは図1に記載しておいた。どうだ、簡単だろう?では先行は私だ」早々にそう言うと悪魔は10円玉の山に手を延ばしはじめた。勘のいいあなたは先攻に必勝法があると確信し、悪魔の伸びきった手を払いのけ「いや、先攻は私だ!」と高らかに主張する。さてその必勝法とは?
数学者の間ではこのような解答は「美しい」とされている。Creative problem solvingという授業では、問題に潜む美しさを探し出すテクニックを数多く学んだ。今日は数学の美しさについてと、それを探し当てるテクニックについて少し話してみたいと思う。
もちろん数学の美しさには明確な定義というものはない。しかしこれ以上簡略化できない洗練された解答が特に美しいと私は思う。その究極とも言えるものが「Proof without words(文字なし証明)」にあたると思う。たとえば学校で習うピタゴラスの定理(三平方の定理)をコメントも使わず三角と四角の図だけで証明してみせたりする。ピタゴラスに限らず他の定理の文字なし証明を集めた本まで出版されているので決してマイナーな世界ではない(そもそも数学自体がマイナーであると言われると身も蓋もないが…)。
逆に「美しくない」解答の例としてよく引き合いにされているのが【四色定理】の解答である(四色定理とは、いかなる地図も、隣接する領域が異なる色になるように塗るには4色あれば十分だという定理である)。この定理は1976年に証明されているが、その際スーパーコンピューターを1200時間も回し続けてようやく証明されたのである*。この強引な証明方法を嫌う数学者は多く、コンピュータを使わない証明方法を探そうとするものも少なくない。しかしそのような方法はまだ見つかっておらず、依然としてコンピューターの計算処理能力に頼らずにはいられないのが現実である。
そもそも何故「美しい解答」にこだわるのか。それは「美しい解答」こそ、問題の本質を見抜いているからと私は思う。問題を十二分に理解しているからこそ無駄を極限までに省いた解答方法が浮かび上がる。さらに、洗練された解答には無駄なところがないため、同じような問題の複雑なバージョンにも応用が利きやすい。ガウスが編み出した計算方法は100までの和を求めるときだけでなく、200までの和を求めるときや、1~Nまでの和を求めるときにも応用ができる。
話は戻るが、私が受けた授業ではまさにこの本質を見抜く練習を多くさせられた。そもそも「ひらめき」が必要な問題に法則があるわけではない。問題によって解き方は異なり、見えてくる美しさも異なる。しかしそれでも無防備に問題へと立ち向かう必要はない。いずれも授業で習った手法ではあるが、問題に立ち向かうためのテクニックを3つ紹介したいと思う:
(1) 簡略化してみる
大きな問題に直面したとき、とりあえずその問題の簡単バージョンについてあれこれ考えてみる。たとえば【1から100の和】の場合、もっと簡略化した【1から10の和】についてまずは考えてみる。これでひらめくかどうかは別として、1から10までの数字であれば容易に紙に書くことができるので、あれこれ試して問題の全体像を把握したいときに役に立つ手法である。
(2) 極端な例を考えてみる
極端を想定すると問題の限界や、時には本質的な部分を垣間見ることが出来る。【丸いテーブルと大量の10円玉硬貨】を極端に考えると「そもそもテーブルのサイズが10円玉と同じサイズだったら、先手必勝は明らかである」。これが意外に、というべきか、より大きなテーブルを想定した時の解決の糸口にもなっている。
(3) とりあえずやってみる
一見当たり前のアドバイスに聞こえるが、これが意外と難しかったりする。なぜなら難題を目の当たりにすると、どこから手をつければいいか分からなくなってしまう。【四色定理】を解いてみろと言われてもどこからスタートするべきか検討がつかない。これは「答えを探す」ことが目的になっているためで、これを「問題を理解する」ことに目標を下げれば意外に手が進む。とりあえず地図をいくつか作ってみて4色に塗ってみる。そうしていくと次にやるべきことは自然と浮かび上がるのである。
その他にも難題に対抗するための武器をCreative problem solvingの授業で学んだのだが、これ以上はマニアックな領域に入りそうなのでここら辺に留めておきたいと思う。冒頭の問題については下に解答を用意しておいたが、折角なので【二人の馬主】問題もおまけとしてシェアしたいと思う。同様にこの問題の解答も下に書いておいたが、「なるほど!」と思う答えなので是非答えを見る前に挑戦していただきたい。
【二人の馬主】
二人の馬主がいる。今日もお互いの馬を競い合うことになっているが、主催者の奇行とも言うべきか、なんと、今日のレースでは二人の馬のどちらか遅いほうの馬に賞金が出るレースとなっている(ある意味、負けるが勝ち)。しかしこのままだと馬主は騎手に対して遅く進むよう指示をだすだろうから、何ともゆったりと、しかも永遠にお互いがゴールをしようともしない退屈なレースになってしまう。どのようにすれば通常の時間内にレースを終わらせられることが出来るのでしょうか?
【答え:丸いテーブルと大量の10円玉硬貨】
まずテーブルのど真ん中(中心点)にコインを置く。悪魔が次にコインを置いたら、その「反対側」にコインを置く。ここで言う「反対側」とは、悪魔の置いたコインを中心点から180度回転させたところである。たとえばテーブルを時計に見立てると、悪魔が時計の3時にコインを置いたら、ぐるっと180度回転した9時に自分のコインを置く(その際、中心点からの距離が同じになるよう気をつける必要がある)、相手が11時に置いたら5時。こうすると悪魔がコインを置けるときは、「反対側」には必ずコインを置くスペースが遺されているので、最後にコインを置けることが保証されている。
【答え:二人の馬主】
騎手を入れ替える。そうすると乗っている馬は相手の馬だから、負けさせるためには最初にゴールしなければならなくなる。
二人の馬主がいる。今日もお互いの馬を競い合うことになっているが、主催者の奇行とも言うべきか、なんと、今日のレースでは二人の馬のどちらか遅いほうの馬に賞金が出るレースとなっている(ある意味、負けるが勝ち)。しかしこのままだと馬主は騎手に対して遅く進むよう指示をだすだろうから、何ともゆったりと、しかも永遠にお互いがゴールをしようともしない退屈なレースになってしまう。どのようにすれば通常の時間内にレースを終わらせられることが出来るのでしょうか?
【答え:丸いテーブルと大量の10円玉硬貨】
まずテーブルのど真ん中(中心点)にコインを置く。悪魔が次にコインを置いたら、その「反対側」にコインを置く。ここで言う「反対側」とは、悪魔の置いたコインを中心点から180度回転させたところである。たとえばテーブルを時計に見立てると、悪魔が時計の3時にコインを置いたら、ぐるっと180度回転した9時に自分のコインを置く(その際、中心点からの距離が同じになるよう気をつける必要がある)、相手が11時に置いたら5時。こうすると悪魔がコインを置けるときは、「反対側」には必ずコインを置くスペースが遺されているので、最後にコインを置けることが保証されている。
【答え:二人の馬主】
騎手を入れ替える。そうすると乗っている馬は相手の馬だから、負けさせるためには最初にゴールしなければならなくなる。
- 1









