地震は確率論では語れない

テレビを見れば大変な惨状。その後も震度5・6級の余震がひっきりなし。あろうことか、16日午前1時半に起きた震度7の揺れが実は本震との気象庁発表が追い打ちをかける。えっ、こんなことがあるの？

自然現象に対して人間が無力であることは、これまでの幾多の経験で共有されているはずなのに、災害が発生するたびに同じことが繰り返される。特に地震に関しては、1995年の「阪神・淡路大震災」、2011年の「東日本大震災」をはじめ、大きな地震が頻繁に発生しているにもかかわらず、学習効果が働いていないように見える。私たちにリスクマネジメントが欠けているだけだろうか？

地震の予知は盛んに行われているが、その精度は極めて低くなっている。当然といえば当然で、自然界の大きさや奥深さと人間の能力がかい離しすぎているのだ。このようなこともあって、我々には大いなる勘違いが蔓延しているように感じる。
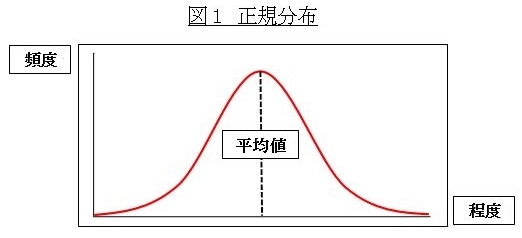
つまり、地震の予知を確率的に起こらないと捉えがちなのだ。確率というのはランダムな現象についてのみ当てはまるものである。そして、ランダムに発生する現象は、通常「正規分布」の形をとる（図1）。正規分布とは、あるサンプル集団のばらつきが、その平均値を境として前後同じ程度にばらついている状態を示し、分布図で見ると、平均値を線対称軸とした左右対称の釣鐘型でなだらかな曲線を描く。そして、平均値から左右に遠くなるほど生起確率は0に近づく。従って、「ランダムに発生する○○の確率は？」という問いに「正規分布」が示す答えには一定の意義がある。

では、地震はどうか？
地震は正規分布の形をとらない。むしろ、「べき分布」の形をとる（図2）。
べき分布とは、平均値からはずれたものが、かなり長く延びている形だ。つまり、極端な値をとるサンプルの数が正規分布より多く、そのため大きな値の方向に向かって曲線は長くなだらかに裾野が伸びていき、正規分布では起こりえない事象が実際にはある程度の頻度で起こってしまうことを表している。

それでは、なぜ地震はべき分布に従うのか？
それは、地震が地殻の歪みという物理的な原因によって発生するメカニズムを持ち、ほぼ規則的におこる性格の自然現象であるからだ。地震はしばらく発生しないと、その歪みが最大化し、その後に大きな地震が発生する。このように、ランダムに起こる現象ではないため、正規分布で表される確率論で捉えるのは適切ではない。

正規分布では「ほぼ100％起こらない」と結論付けられる地震が、ある一定の頻度で起こっていることは、そのことを物語っている。例えば、活断層型の大地震は数千年ごとに起こると言われている。この自然界の法則性を人間の時間スケールでは「規則的に地震は起こる」とは認識できないのだ。本当は「今日起こるかもわからないし、千年後に起こるかもわからない」リスクを「地震は起こらない」と判断してしまう。そして、災害への備えも疎かになる。

地震で想定外は許されない

地震の発生は「正規分布」によらず、「べき分布」に従うと仮定すれば、今日の地震の予測手法は科学的・統計的に必ずしも正しいとは言えない。もしそうであれば、科学的な予測の範疇を超えた災害が起こった場合、それは想定外とみなしていいものだろうか？
　
　予測の手法が誤っていれば、当然得られた結論にも根拠はないはずである。人知を超えて発生する災害へのリスクマネジメントは、科学万能を排し、より最悪の結果を念頭に置くべきである。特に地震の予知情報から「想定外」が導かれてはならない。そもそも、この地震列島で大地震から逃れられる安全な地域などないのである。

　寺田寅彦がこんな言葉を残している。現代人にとって、忘れてはならない箴言であろう。

『「自然」は過去の習慣に忠実である。地震や津浪は新思想の流行などには委細かまわず、頑固に、保守的に執念深くやって来るのである。紀元前二十世紀にあったことが紀元二十世紀にも全く同じように行われるのである。科学の方則とは畢竟「自然の記憶の覚え書き」である。自然ほど伝統に忠実なものはないのである。』（昭和8年5月「鉄塔」）